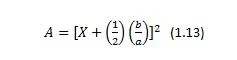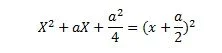Tam adı; Ebu Abdullah Muhammed İbni Musa El Harezmi. Genel kabulle Ortaçağ İslam dünyasının en büyük bilimsel yeteneklerinden biri! Batı Türkistan’da ki Aral gölü güneyinde bulunan Harezm bölgesinde 780 yılında dünyaya gelip, 850 ‘de da Bağdat’ta vefat etmiştir.
Üç oğlu vardır ve hepsi de matematik üzerinde çok önemli çalışmalar yapmışlardır.Çağına göre üstün özellikler taşıyan eserlerinin en ilginç yönlerden birisi de, açıların sinüs gibi trigonometrik fonksiyonlarla ifade edildiğini gösteren bazı tabloların bulunmasıdır.10. yüzyılda yaşıyan ve tüm dünyaya isminin (El Harezmi – Al Khrawarizmi) Latince telaffuzunu “algoritma” olarak zikrettiren bu Müslüman Türk alimi, cebir matematiğinin de kurucusudur.
Zaten cebir kelimesi de Harezmi’nin (El Kitab’ül Muhtasar Fi Hisab’il Cebri ve’l Mukabele ) “Cebir ve denklem hesabı üzerine özet kitap” adlı eserinden gelir.Harezmi, cebir denklemlerinin çözümünde kare ve diktörgen şekillerden yararlanır.
Denklem çözümlerinde bu geometrik şekilleri kullandığından , denklemlerde hep artı işaretli terimler göz önünde tutulur.Kare bilinmeyeni, dikdörtgen ise bilinmeyenin sabit bir katını temsil eder. Denklem çözümleri daima pozitif değerler içindir.
El-Harezmi, ikinci dereceden denklemlerin çözülmesi için geometrik modeller de kullanır.Fakat bu çözümleme yöntemleri, malesef ki Türkiyede neredeyse hiç bir ders kitabında gösterilmez. İkinci derece denklemlerin çözümünü çok sade, anlaşılır ve sistematik biçimde yazmıştır.
Çözümleri adım adım sistemli bir sıra ile vermiş olması, – isminin Latince telaffuzu ile - ‘algoritma’ yöntemlerinin ortaya çıkması sağlamıştır.
Günümüzde dünyasının vazgeçilmez parçası bilgisayarların programlama dilleri, Harezmi’nin algoritmik yöntemleri esas alınarak yazılmaktadır. Dolayısı ile günümüz programcılığının ve daha bir çok şeyin temelinde Harezmi’nin de olduğunu söylemek mümkündür.
El-Harezmi ikinci dereceden olan ve birinci tip diye kümelediği denklemlerin genel ifadesi:

Şeklinde sol tarafında ikinci ve birinci dereceden bilinmeyenleri, sağ tarafında da sabit terimi ihtiva eder. El-Harezmi bunun çözümü için birbirinden farklı iki yöntem önermiştir. Bunlar,
1) Önce terimi geometrik olarak bir kenar X olan, Şekil 1’deki ABCD ile gösterilen bir kareyi ifade ettiği düşünülür.

Denklem 1.1’in sol tarafındaki birinci dereceden bilinmeyen, yani ikinci terim bir kenarı X ve yüksekliği a olan bir dikdörtgeni gösterir. Şekil 1.1’de simetrikliği sağlamak için alanı aX olan bu dikdörtgeni ABCD karesinin her kenarına eşit dağıtabilmek için X kenarının uzunluğu aynı kalacak ve yüksekliği a/4 olacak şekilde içi taralı dört tane dikdörtgen ilave edilir. Böylece, ortaya çıkan en dıştaki noktalı çizgilerle gösterilmiş olan en büyük karenin alanı, A, dört köşede beliren küçüj noktalı karelerinin de göz önünde tutulması ile,

Olur. Diğer taraftan, en büyük karenin alanı bir kenarın uzunluğu cinsinden yazılacak olursa aşağıdaki alan ifadesi elde edilir.

İşte bu son iki denklem birbirine eşit olduğundan

Yazılabilir. Denklem (1.3)’in göz önünde tutulması ile bu son ifadenin sol tarafındaki ilk iki terimin toplamının b olduğu anlaşılır. Burada da,

Elde edilir. Burada, bilinmeyen terimi sadece eşitliğin bir tarafında kalan bir ifadeye ulaşılır. Son olarak, karekök alınarak gerekli düzeltmelerin yapılması ile

Çözümleri elde edilir.
2) Burada yine aşağıdaki şekilde ABCD ile gösterilen bir kare ile temsil edilir. Yine daha büyük ve tam bir kare elde edebilmek için bu temel kare, Denklem(1.1)’deki aX terimini temsil edebilmek için bir yatay, bir de düşey kenarı uzunluğunda uzatılırsa ortaya iki adet taralı ve her birinin alanı (a/2)X olan dikdörtgenler çıkar. Bu taralı iki dikdörtgenin alanlarının toplamı aX’dir. Böylece ABCD karesi ile taralı iki dikdörtgenin alanlarının toplamı bize Denklem (1.1)’in sol tarafındaki bilinmeyenli terimlerinin toplamını verir. Bu üç alanı da içine alan ve kenar uzunluğunu olan en büyük karenin alanı,

Olarak bulunur.

Aslında en büyük kare alanı biri karesini, ikisi dikdörtgenlerini ve sonuncusunu da Şekil 1.2’de noktalı kenarla gösterilen karesini içeriri. Buna göre, en büyük kareinin cebirsel alanını

Şeklinde yazılır. Son iki ifadenin birbirine eşit olmaları sebebi ile

yazılır. Bu ifadenin sol tarafındaki iki tane X bilinmeyenin ihtiva eden terimlerin toplamını Denklem(1.1)’i göz önünde tutarak yeniden yazarsak

Denklemi elde edilir ki, bu da, birinci çözüzmde elde edilen (1.+) denkleminin aynısıdır. O halde, göz önünde tutulan (1.1) denklemindeki ikinci dereceden bilinmeyenli denkleminin kökleri (1.5) ve (1.6) denklemleri ile verilir.
El-Harezmi en genel hali ile aşağıdaki ikinci dereceden denklemin köklerinin çözümünü düşünmüştür. Uzun uğraşılar sonrasında, aklına geometrik bir modelin öncelikle incelene olay esas alınarak kurulmasının gerektiğini düşünmüştür. Denklem, en genel halinde a,b ve c katsayıları ile ve X bilinmeyeni içeren

Şeklinde cebirsel olarak yazılabilir. İnsanın aklına buradaki X2 terimin kenarı X’e eşit olan bir kare oldığı gelmektedir. O halde, bilinmeyen karesi yani X2 geometrik olarak kare ile temsil edilebilir. El-Harezmi önce denklemin her iki tarafını a ile bölerek ilk terimin bir kenarı X olankare haline dönüşmesini sağlamıştır.

Şekil (1.1)’ de X2 terimi kare alan olarak gösterilmiştir. İlk terim bir alanla temsil edildiğine göre diğerlerinin de alanlarla ifade edilmesi gerekir ki modelde esas alınan büylüklüğü sağlayabilelim.

İkinci terim de bir alan olarak düşünülmesi, birinci terimdeki kareinin kenarı X olduğunda göre, ikinci terimi bir kenarı bu kare ile ortak diğer kenarı da X+(1/2)(b/a) olan bir dikdörtgenle modelleyebiliriz. (Şekil 1.3)
Böylece şekilde gösterildiği üzerE kenarları olan daha büyük bir kare meydana çıkar. Bu karenin alanı, A, alt alanlarının toplamına eşittir. Alt alanlar ikisi farklı yüzey alanlı kare, diğer ikisi de birbirinin aynı alana sahip dikdörtgen olmak üzere 4 tanedir. Toplam alan

dir. Denklem (1.3)’deki toplam alanın ilk iki terimi (1.8) denkleminin ilk iki terimin aynısıdır Toplam kare alanı

şeklinde yazılabilir. Böylece, Denklem (1.12) ve (1.13) birbirine eşdeğerdir. Buna göre,

Denklem (1.11)’ye benzer bir ifade elde etmek için bu son denklemin her iki tarafına (c/a) ilave edersek eşitlik bozulmaz

Elde edilir. Ancak sol taraftaki ilk üç terimin toplamı (1.11) eşitliğine göre sıfır olduğundan elimizde

kalır. Her iki tarafın karekökünün alınmasıyla

elde edilir. Buradan da sonuç olarak iki kök

bulunur. Böylece ikinci dereceden bir denklemin kökleri bulunmuş olunur.
Aşağıdaki linkten konusuna ulaşabilirsiniz..;
El-Harezmi ve Çalınan Türk Tarihi
Üç oğlu vardır ve hepsi de matematik üzerinde çok önemli çalışmalar yapmışlardır.Çağına göre üstün özellikler taşıyan eserlerinin en ilginç yönlerden birisi de, açıların sinüs gibi trigonometrik fonksiyonlarla ifade edildiğini gösteren bazı tabloların bulunmasıdır.10. yüzyılda yaşıyan ve tüm dünyaya isminin (El Harezmi – Al Khrawarizmi) Latince telaffuzunu “algoritma” olarak zikrettiren bu Müslüman Türk alimi, cebir matematiğinin de kurucusudur.
Zaten cebir kelimesi de Harezmi’nin (El Kitab’ül Muhtasar Fi Hisab’il Cebri ve’l Mukabele ) “Cebir ve denklem hesabı üzerine özet kitap” adlı eserinden gelir.Harezmi, cebir denklemlerinin çözümünde kare ve diktörgen şekillerden yararlanır.
Denklem çözümlerinde bu geometrik şekilleri kullandığından , denklemlerde hep artı işaretli terimler göz önünde tutulur.Kare bilinmeyeni, dikdörtgen ise bilinmeyenin sabit bir katını temsil eder. Denklem çözümleri daima pozitif değerler içindir.
El-Harezmi, ikinci dereceden denklemlerin çözülmesi için geometrik modeller de kullanır.Fakat bu çözümleme yöntemleri, malesef ki Türkiyede neredeyse hiç bir ders kitabında gösterilmez. İkinci derece denklemlerin çözümünü çok sade, anlaşılır ve sistematik biçimde yazmıştır.
Çözümleri adım adım sistemli bir sıra ile vermiş olması, – isminin Latince telaffuzu ile - ‘algoritma’ yöntemlerinin ortaya çıkması sağlamıştır.
Günümüzde dünyasının vazgeçilmez parçası bilgisayarların programlama dilleri, Harezmi’nin algoritmik yöntemleri esas alınarak yazılmaktadır. Dolayısı ile günümüz programcılığının ve daha bir çok şeyin temelinde Harezmi’nin de olduğunu söylemek mümkündür.
BİRİNCİ DERECEDEN DENKLEM ÇÖZME METODU
El-Harezmi ikinci dereceden olan ve birinci tip diye kümelediği denklemlerin genel ifadesi:
denklem-1.1.jpg
Şeklinde sol tarafında ikinci ve birinci dereceden bilinmeyenleri, sağ tarafında da sabit terimi ihtiva eder. El-Harezmi bunun çözümü için birbirinden farklı iki yöntem önermiştir. Bunlar,
1) Önce terimi geometrik olarak bir kenar X olan, Şekil 1’deki ABCD ile gösterilen bir kareyi ifade ettiği düşünülür.
sekil-1.1.jpg
Denklem 1.1’in sol tarafındaki birinci dereceden bilinmeyen, yani ikinci terim bir kenarı X ve yüksekliği a olan bir dikdörtgeni gösterir. Şekil 1.1’de simetrikliği sağlamak için alanı aX olan bu dikdörtgeni ABCD karesinin her kenarına eşit dağıtabilmek için X kenarının uzunluğu aynı kalacak ve yüksekliği a/4 olacak şekilde içi taralı dört tane dikdörtgen ilave edilir. Böylece, ortaya çıkan en dıştaki noktalı çizgilerle gösterilmiş olan en büyük karenin alanı, A, dört köşede beliren küçüj noktalı karelerinin de göz önünde tutulması ile,
denklem-1.2.jpg
Olur. Diğer taraftan, en büyük karenin alanı bir kenarın uzunluğu cinsinden yazılacak olursa aşağıdaki alan ifadesi elde edilir.
denklem-1.3.jpg
İşte bu son iki denklem birbirine eşit olduğundan
denklem-1.3.1.jpg
Yazılabilir. Denklem (1.3)’in göz önünde tutulması ile bu son ifadenin sol tarafındaki ilk iki terimin toplamının b olduğu anlaşılır. Burada da,
denklem-1.4.jpg
Elde edilir. Burada, bilinmeyen terimi sadece eşitliğin bir tarafında kalan bir ifadeye ulaşılır. Son olarak, karekök alınarak gerekli düzeltmelerin yapılması ile
denklem-1.5-1.6.jpg
Çözümleri elde edilir.
2) Burada yine aşağıdaki şekilde ABCD ile gösterilen bir kare ile temsil edilir. Yine daha büyük ve tam bir kare elde edebilmek için bu temel kare, Denklem(1.1)’deki aX terimini temsil edebilmek için bir yatay, bir de düşey kenarı uzunluğunda uzatılırsa ortaya iki adet taralı ve her birinin alanı (a/2)X olan dikdörtgenler çıkar. Bu taralı iki dikdörtgenin alanlarının toplamı aX’dir. Böylece ABCD karesi ile taralı iki dikdörtgenin alanlarının toplamı bize Denklem (1.1)’in sol tarafındaki bilinmeyenli terimlerinin toplamını verir. Bu üç alanı da içine alan ve kenar uzunluğunu olan en büyük karenin alanı,
denklem-1.7.jpg
Olarak bulunur.
sekil-1.2.jpg
Aslında en büyük kare alanı biri karesini, ikisi dikdörtgenlerini ve sonuncusunu da Şekil 1.2’de noktalı kenarla gösterilen karesini içeriri. Buna göre, en büyük kareinin cebirsel alanını
denklem-1.8.jpg
Şeklinde yazılır. Son iki ifadenin birbirine eşit olmaları sebebi ile
denklem-1.8.1.jpg
yazılır. Bu ifadenin sol tarafındaki iki tane X bilinmeyenin ihtiva eden terimlerin toplamını Denklem(1.1)’i göz önünde tutarak yeniden yazarsak
denklem-1.9.jpg
Denklemi elde edilir ki, bu da, birinci çözüzmde elde edilen (1.+) denkleminin aynısıdır. O halde, göz önünde tutulan (1.1) denklemindeki ikinci dereceden bilinmeyenli denkleminin kökleri (1.5) ve (1.6) denklemleri ile verilir.
İKİNCİ DERECEDEN DENKLEM ÇÖZME METODU
El-Harezmi en genel hali ile aşağıdaki ikinci dereceden denklemin köklerinin çözümünü düşünmüştür. Uzun uğraşılar sonrasında, aklına geometrik bir modelin öncelikle incelene olay esas alınarak kurulmasının gerektiğini düşünmüştür. Denklem, en genel halinde a,b ve c katsayıları ile ve X bilinmeyeni içeren
denklem-1.10.jpg
Şeklinde cebirsel olarak yazılabilir. İnsanın aklına buradaki X2 terimin kenarı X’e eşit olan bir kare oldığı gelmektedir. O halde, bilinmeyen karesi yani X2 geometrik olarak kare ile temsil edilebilir. El-Harezmi önce denklemin her iki tarafını a ile bölerek ilk terimin bir kenarı X olankare haline dönüşmesini sağlamıştır.
denklem-1.11.jpg
Şekil (1.1)’ de X2 terimi kare alan olarak gösterilmiştir. İlk terim bir alanla temsil edildiğine göre diğerlerinin de alanlarla ifade edilmesi gerekir ki modelde esas alınan büylüklüğü sağlayabilelim.
sekil-1.3.jpg
İkinci terim de bir alan olarak düşünülmesi, birinci terimdeki kareinin kenarı X olduğunda göre, ikinci terimi bir kenarı bu kare ile ortak diğer kenarı da X+(1/2)(b/a) olan bir dikdörtgenle modelleyebiliriz. (Şekil 1.3)
Böylece şekilde gösterildiği üzerE kenarları olan daha büyük bir kare meydana çıkar. Bu karenin alanı, A, alt alanlarının toplamına eşittir. Alt alanlar ikisi farklı yüzey alanlı kare, diğer ikisi de birbirinin aynı alana sahip dikdörtgen olmak üzere 4 tanedir. Toplam alan
denklem-1.12.jpg
dir. Denklem (1.3)’deki toplam alanın ilk iki terimi (1.8) denkleminin ilk iki terimin aynısıdır Toplam kare alanı
denklem-1.13.jpg
şeklinde yazılabilir. Böylece, Denklem (1.12) ve (1.13) birbirine eşdeğerdir. Buna göre,
denklem-1.13.1.jpg
Denklem (1.11)’ye benzer bir ifade elde etmek için bu son denklemin her iki tarafına (c/a) ilave edersek eşitlik bozulmaz
denklem-1.13.2.jpg
Elde edilir. Ancak sol taraftaki ilk üç terimin toplamı (1.11) eşitliğine göre sıfır olduğundan elimizde
denklem-1.13.3.jpg
kalır. Her iki tarafın karekökünün alınmasıyla
denklem-1.13.4.jpg
elde edilir. Buradan da sonuç olarak iki kök
denklem-1.14-1.15.jpg
bulunur. Böylece ikinci dereceden bir denklemin kökleri bulunmuş olunur.
Aşağıdaki linkten konusuna ulaşabilirsiniz..;
El-Harezmi ve Çalınan Türk Tarihi